RPAS Mission Planning
RPAS are nowadays more being used even by hobbyists to generate orthographic imagery for mapping purposes.
While arguably controlling remotely piloted aerial systems is more or less automated these days with modern technology, there's still a lot of skills, planning and considerations for any operator to take into account. In mountainous regions even more so, especially when it comes to quality, accuracy, level of detail and most importantly in areas with significant variation in elevation the consistency.
While for some contributors quality of data is totally irrelevant, just add any data anywhere within a certain area and that's totally fine - for instance a shop inside a building, add that node anywhere within the area of that building, it doesn't have to be accurate - other mappers may wish to work as accurate as possible with current hobbyist and semi-professional equipment to contribute to OpenStreetMap guarantee consistency of the quality of data they process and upload to OpenStreetMap.
This article is for the latter contributors for which data accuracy is relevant and of course one needs to rely on the same accuracy in the original source of the information.
Since quality, level of detail and accuracy plays a significant role in mapping practice by those who wish to achieve the best accuracy they can and while at the same time any good survey starts in the planning phase we decided to share our experiences and the math behind good mission planning to generate the best achievable orthographic imagery as a result of RPAS surveys to be used for tracing polygons for OpenStreetMap.
Sadly there's some math involved in good mission planning and quite some hobbyist RPAS operators find this part daunting and rely on the "belly guessing" approach for settings within the app, so this article will help the both the hobby and professional mappers or surveyors to achieve consistency in quality and accuracy of data by showing the math and formulas to be able to achieve the right settings in your RPA controller application/device.
Added is a table with resulting data for the most common settings we're using in our RPAS application/controller but since every mappers/surveyor RPAS operator might have their own settings for conducting RPAS surveys we add the math behind the tables as well so you can always calculate the right values for any custom requirements you personally have for your contributions to OpenStreetMap.
Area planning
Take-off location
Flight planning
Flight directions
Terrain elevation adjustments
In our city we have a lot of variations in the landscape, of which most notably the elevations. Our lowest point in the city is at around 920 meters at the Bued river down Kennon Road towards Camp 6, with to the northwest very steep incline going up some 300 meters in elevation in roughly 400 meters horizontal movement.
The highest point in the city is at Busol Watershed, left of the road towards Beckel, La Trinidad and rises to 1670m elevation.
Because of this relief in the landscape, apart from Central Business District, there's hardly any flat area in the city and this has significant impact on planning the surveys for the drone to get not only sharp images but also with the proper level of detail and accuracy.
In our experience both the decrease in sharpness and level of detail is detrimental to the resulting accuracy in orthographic images.
The rationale is that in our experience using our equipment and the fulfillment of NAMRIA standard that data should be <10cm accuracy, this to be achieved at flying 60m height and 80% overlap both "Front" and "Side", at these settings we achieve mostly 1-3cm accuracy, with proper level of detail, sharpness and light conditions for the imagery. Thus weather conditions do impact the quality of a survey and therefore also impact accuracy. We assume for the rationale here optimal conditions.
Under optimal conditions our experience with our equipment shows we need a minimum of some 50% overlap to stay within the 10cm accuracy.
So this begs the question, how to guarantee that?
Assume the RPAV is flying at some 60m height and 80% overlap to the lowest point, what would be the boundary of the highest point in the area to be surveyed to maintain at least 50% overlap?
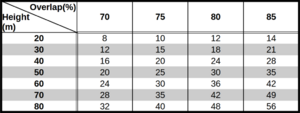
On the right is a table with common values for those who wish to skip calculations, for custom values use the formula below.
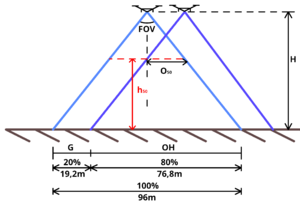
Below is the equation for this and the explanation how to get to this simple formula while the image on the right shows the visualization of the rationale.
From the image on the right we can deduct the three basic formulas
1) tan(½ • FOV) = G/(H-h50)
2) tan(½ • FOV) = V1/H ⇒ V1 = H • tan(½ • FOV)
3) G = 2 • V1 • (1 - OH)
4) 3→1 ⇒ 2 • V1 • (1 - OH)/(H - H50)=tan(½ • FOV)
5) 2→4 ⇒ 2 • H • tan(½ • FOV) • (1 - OH)/(H - h50) = tan(½ • FOV)
⇒ 2 • H • (1 - OH)/(H - h50) = 1
⇒ 2 • H • (1 - OH) = H - H50
⇒ H - 2 • H • (1 - OH) = H50
⇒ H50 = H (1 - 2 • (1 - OH))
In our case where we wish to fly the drone at H = 60m above the lowest ground level at OH = 80% (0,8) Overlapping at lowest ground level, that means to ensure minimum 50% overlap the maximum of H50 is then 36 meters
note this formula also easily gives you a clue that if locations in the area to be surveyed are 40 or 42m, you can either relocate to a higher elevation as your base point (split the survey into sub-areas) or with OH = 85% then H50 becomes 42 meters
At OH = 90% then H50 becomes 48m, but keep in mind flight time is twice as long now as at OH = 80% so relocating might be a more time-effective solution.
Minimum overlap based on the take-off height of the platform from which we conduct our survey
For our project we wish 80% for both "Front" and "Side" overlaps at an flight-height of 60m above the ground as the base for our surveys.
Due to the CAAP[1] regulations[2] in our country mandating us to always keep a clear visible line-of-sight we usually have to get on top of a view deck, building, water tank or any other platform from which to conduct the survey.
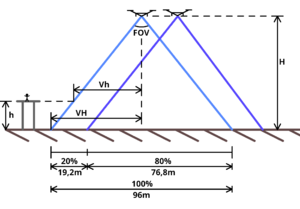
In the "Take-off elevation" image to the right, you'll find the following parameters (not all are relevant to the final formula, but mentioned for the peer-reviewing process):
| Variable | Description |
|---|---|
| ● FOV | Field of View angle, this information is presented to you with the specifications of the drone you bought. For the Mavic 2 Pro it's 77°[3] |
| ● H | Height of the drone above the terrain you wish to survey |
| ● h | Height of the platform from which the RPAV is taking off, this can be at the top of any platform such as a building |
| ● VH | Width of the terrain within the view of the camera |
| ● Vh | Width of view at the elevation of the take-off platform for the camera |
| ● OH | Overlap at height H |
| ● Oh | Overlap at height h |
tan(½ • FOV) = VH/H => VH = H • tan(½ • FOV)
in our case the tangent of ½ • 77° amounts to roughly rounded 0,8 thus with an H of 60m results to 48m
2 • VH is the total view resulting in 96m
At an 80% Overlap "OH" as indicated in the image, out of 96m results in 19,2m which we consider the Gap "G" between the edges of neighbouring images. In factor G = 1 - OH or in percentages G = 100 - OH
Simple math dictates (H - h)/Vh = H/VH => Vh = VH • (H - h)/H
To maintain the same G and overlap at terrain level the drone moves between the "Front" and "Side" with the same shift which equals G. Since the angle FOV is constant, regardless of h, it means the overlap at height "Oh" is then (1 - G/Vh)
So we can conclude that Oh = (1 - G/Vh) and Vh = VH • (H - h)/H results to Oh = 1 - G/(VH• (H - h)/H) => Oh = 1 - (G • H)/(VH•(H - h))
We know that G is defined as (1 - OH) • VH which then results to Oh = 1 - ((1 - OH) • VH • H)/(VH • (H - h)) And we can eliminate VH at this point obviously to the final solution
Formula Heightoverlap: Oh = 1 - ((1 - OH) • H/(H - h))
How to practically use this formula
If we wish to conduct a survey of the terrain with a RPAV at 60m above the ground and an overlap of 80%, but for the CAAP mandated requirement of uninterrupted "line of sight" during the survey we go to a rooftop or platform 20m above the terrain, then h=20, H=60 and OH=0.8 and as a result in our application for the drone we set the flight height now to H-h is 40m only and the Oh (overlap) according to our formula to be set in the application becomes 0.7 or in percentage 70%
So while standing on a platform at 20m, and setting the flight height to 40m and an overlap of 70% equals then on the ground at 20m below your feet an 80% overlap.
And if you were to find a location 40m above the terrain, the overlap would have to be set to 40% to achieve at ground level an 80% overlap.
Evidently if H-h becomes in this case smaller than 12, then H/(H-h) becomes 5 and the overlap turns to 0%, clearly indicating that at h equals 48m is your boundary, you can't go higher to achieve an 80% overlap, as in that's a physical boundary for this scenario.