User:Alexandre Magno/Rascunho de Tutorial/Extrudando áreas com o JOSM
Extrudar é um termo estranho para a grande maioria das pessoas. Ele tem sua aplicação mais comum na produção de componentes mecânicos. Apesar de serem noções diferentes, talvez seja de lá que ele passa a ser reutilizado em CAD, por operadores dos famosos softwares AutoCAD e Blender.
Em mapeamento OpenStreetMap, utilizando-se o editor JOSM, "extrudar" passa a ter um significado preciso, como operação simples e fácil de executar. Cenários problemáticos que podem requerê-la tornam-se complicados devido à diversidade geométrica que normalmente existe nos mapas.
O problema
Alguns mapeadores não consideram linhas de ruas como eixos e, ao mapear áreas tais como praças e outros terrenos entre ruas, pela comodidade do momento, aproveitam erradamente os pontos de interseção entre as ruas do contorno que se cruzam ou se encontram. Dessa forma, o mapeador acaba por criar uma área que é imperceptível como objeto distinto: seus lados coincidem com segmentos das ruas, que tornam-se seus limites. Pior: seus pontos de vértices estão todos "grudados" a pontos que pertencem às linhas daquelas ruas. Torna-se impossível alterar a geometria da rua sem alterar a geometria da área, e vice-versa. Como se passassem a compartilhar os mesmos segmentos; mas o que acontece é que os pontos (vértices) estão grudados.
Essa situação é mostrada através das três primeiras imagens da seção #Último ensaio: não é prático mas é fácil.
Ligar tão fortemente a geometria de coisas completamente diferentes, geralmente só atrapalha. Dificulta a manutenção do mapa. É errado, porque a área de uma praça não deve invadir ficticiamente a área física da rua. Não se mapeia área de rua no OpenStreetMap, mas os estilos CSS usados na renderização dos tiles cuidam de mascarar o pequeno vazio alargando os eixos (ruas) até parecerem que tem área. "No mapa, a linha é grossa."
Este tutorial ensina a consertar as coisas. Pode haver situações fáceis e situações muito mais difíceis, ou trabalhosas.
Desgrudar, mover e extrudar
Nesta seção, para revisarmos muito brevemente o que é a "extrusão" no editor JOSM, vamos usar o recurso numa área de praça fictícia que, apesar de traçada corretamente, o foi em duplicidade. Usaremos extrusão apenas para redimensionar a segunda forma, mostrando duas extrusões muito simples.
Extrudar ruas para mover e extrudar a área
Voltemos ao problema das "praças artísticas". Geralmente são praças, mas pode acontecer com áreas que não sejam etiquetadas leisure=park. Acontece mais com praças porque quase sempre elas localizam-se entre ruas, sendo tentador ao mapeador inexperiente fazer com que toda a área fique verdinha.
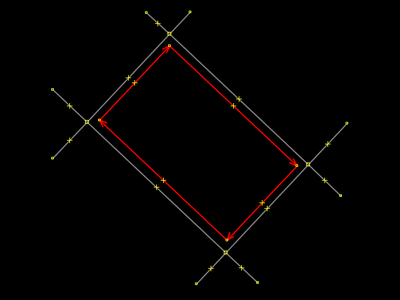
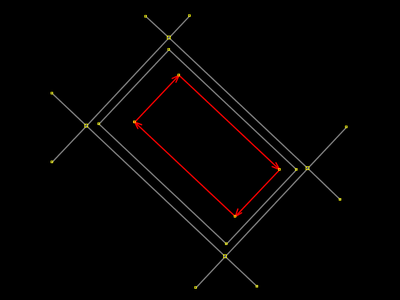
Na imagem, duas ruas paralelas cruzam duas outras ruas paralelas. Todos os ângulos são retos. No meio, o mapeador demarcou a área. Imaginemos que seja uma praça. O operador usou cada um dos quatros pontos que fazem as intereseções entre as ruas. Os softwares editores — iD e JOSM — facilitam essa reutilização de pontos que nem sempre é desejada. Eles aproximam automaticamente o clique do operador para a exatidão do ponto que já fora utilizado antes (na modelagem da interseção/conexão das ruas). A nossa imagem ao lado não mostra, mas ali já está o que aparece selecionado na imagem do passo seguinte. É disso que os parágrafos acima falam. |
|
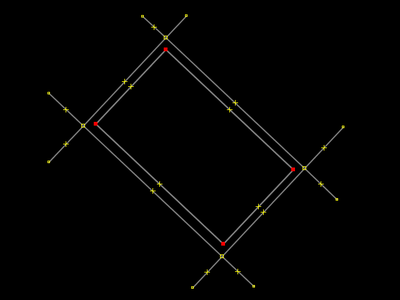
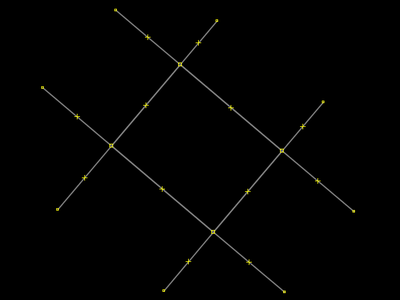
Na situação que estamos estudando, nem sempre o mapeador que opera o JOSM consegue selecionar a área tal como é mostrado agora. Por vezes ele tenta clicar algum lado retângulo mas seleção nunca fica para área, e sim para a rua, como no passo 3, ou para o lado. Se uma seleção de área fosse sempre possível e fácil de obter, a orientação seria simplesmente desgrudar a área para movê-la e alterá-la, como ensinado em #Desgrudar, mover e extrudar. Mas já que as coisas podem não ficar tão fáceis assim, vamos com esse tutorial analisar algumas situações e conhecer soluções. |
|
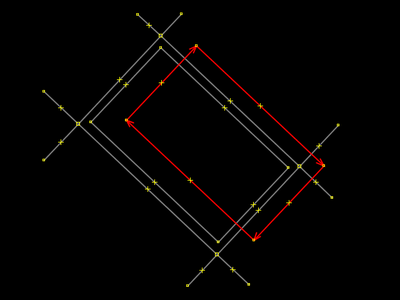
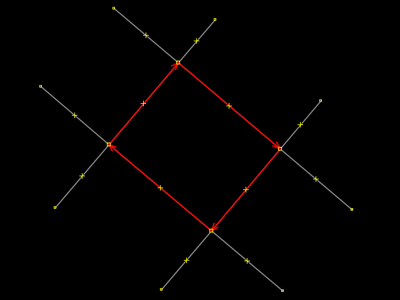
Selecione a rua evitando clicar o lado da área. Se você clica o lado da área, pode acontecer da rua ser selecionada, como já vimos. Mas isso fica na sorte. O JOSM detecta imprecisamente o que o operador está querendo quando clica o lado de uma área como a exemplificada. Ora o JOSM retorna seleção da área, ora ele retorna seleção da rua. Em outros casos, quando as ruas que abstraímos (com seus nomes de rua e formas físicas retilíneas) não são exatamente as retas que vemos no projeto do JOSM, mas são conjuntos de seguementos grudados nos quatro pontos de interseção, o programa pode nem selecionar área nem selecionar rua, mas selecionar o conjunto de segmentos correspondente. |
|
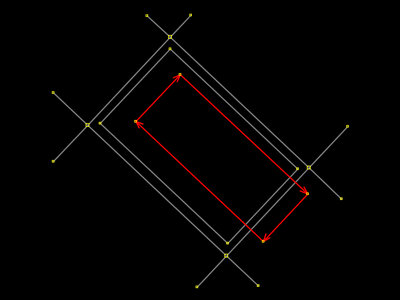
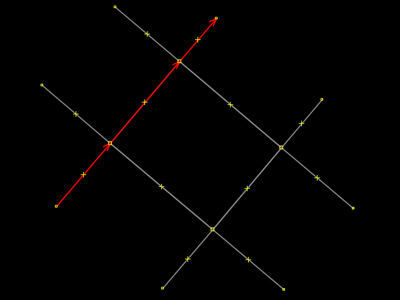
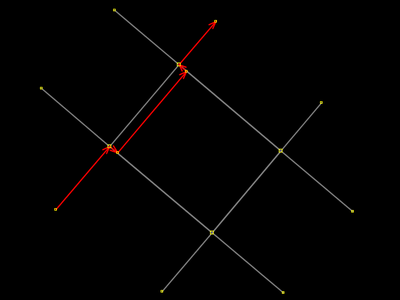
Selecionou-se a linha de rua (reta) e utilizou-se a ferramenta Extrudar com o seguemento dela que coincide visualmente com lado do retângulo. A extrusão foi feita para dentro do retângulo, mas não trata-se de fato do lado do retângulo como era o caso em nossos primeiros exemplos (seção anterior). A seleção denuncia isso. Numa situação de mapeamento real, se você tem dúvida, confronte o conjunto de etiquetas de suas seleções, se eles difererem. |
|
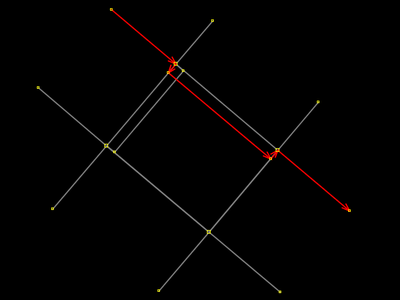
Fez-se o mesmo que no passo 4, só que agora com outra linha de rua (reta). O objetivo com esses dois movimentos é chegar ao ponto de interseção do passo 9, ou 7. Vamos com calma, passa-a-passo, para entender e perceber alguns detalhes. A desvantagem dessa estratégia é que não se extruda uma área de praça, como é proposta do tutorial. Com ela, faz extrusão nas ruas. Então caminha-se para a criação de uma área virtual (visual) com os seguementos das ruas. A etiquetação fica toda confusa, porque a etiquetação dos componentes (lados) da nova área visual é a etiquetação mixada das ruas, enquanto a etiquetação do que não foi movido corresponde ao retângulo que era pra ser extrudado. Invés de chegar ao passo 9, essa estratégia ainda poderia ser modificada para que voltarmos a trabalhar com a área e abandonar as ruas. Isso será realizado em outra sequência. |
|
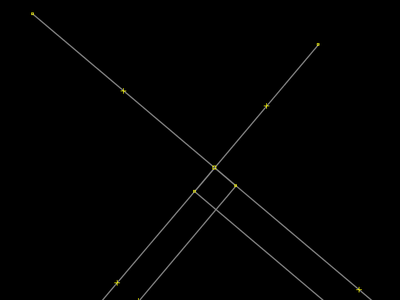
Nada está selecionado. Perceba que não há ponto de interseção entre os dois seguementos de rua que foram extrudados para dentro de nosso retângulo visual. Falamos de "retângulo visual" porque deixamos de trabalhar com o retângulo real para trabalhar com as ruas. Como explicado no passo anterior, a área da praça, ou seja, a área que estamos assumindo ser uma praça e que corresponde ao caminho fechado que aparece selecionado no passo 2, permanece intacta. |
|
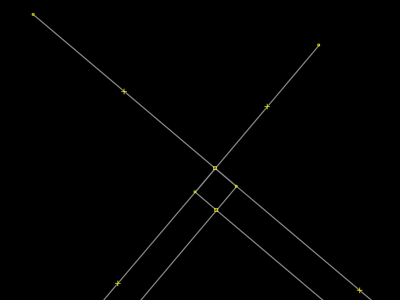
O operador do JOSM — eu, você — força a intereseção, criando o ponto que a faz automaticamente. O JOSM aproxima o clique para o ponto preciso de interseção. Na verdade, quando se clica o ponto visual (ponto ainda imaginário, no plano cartesiano) que corresponderá ao ponto de interseção entre os dois seguementos que se cruzam, é como se o JOSM criasse dois elementos ponto e grudasse eles. Você tem um único ponto, mas que arrasta os dois seguementos. Dica rápida: você clica para criar o primeiro ponto e logo em seguida aperta Esc para desistir de criar um segundo ponto num segundo clique (que você não fará). Do contrário, criaria ao menos um seguemento invés de apenas o ponto que queremos. |
|
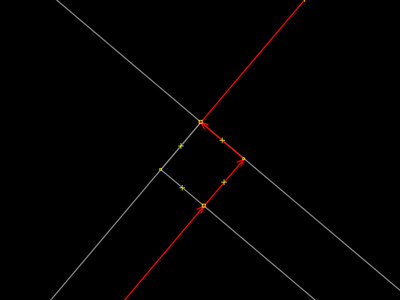
O problema é que a seleção possível a partir do extrudado é somente das ruas, que deixaram de ser retas. Logimente, pois extrudamos as ruas, e não a área. |
|
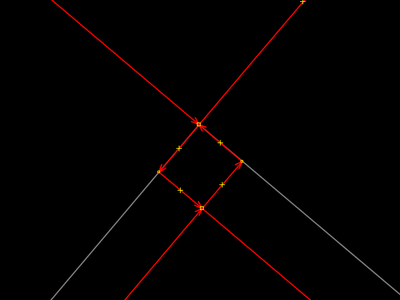
Vê-se que tal estratégia, por ela mesma, é infrutífera. De nada adianta selecionar as duas ruas que agora se cruzam também no segundo ponto que criamos. |
|
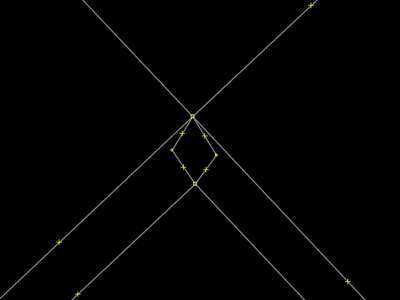
A solução está nos outros dois pontos. A imagem ao lado mostra eles já movidos para uma posição mais interessantes. Aqueles pontos podem ser movidos porque nos momentos das respectivas extrusões dos lados do retângulo eles apenas foram deslocados. Um passo antes já haviam sido desgrudados na interseção das duas ruas. |
|
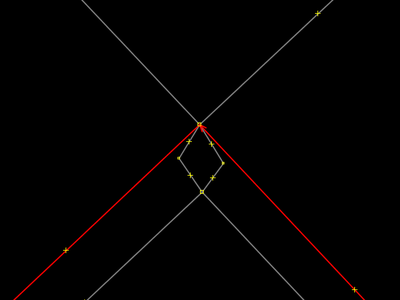
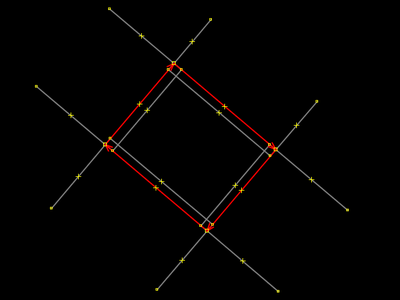
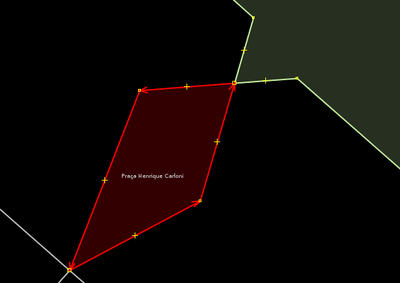
O movimento dos pontos no passo anterior serve para você perceber mais facilmente que pode fazer esta seleção de área que é mostrada ao lado. Na realidade, a imagem não mostra toda a área, mas sabemos, pelas outras imagens da sequência, que o selecionado é um caminho fechado, mais especificamente, a "praça traçada errado" que estamos imaginando para o nosso exemplo em questão. Para selecionar a área, o operador apenas clica um dos quatro lados do retângulo. Note que ele ainda está grudado a cada uma das quatro interseções de rua (pontos). |
|
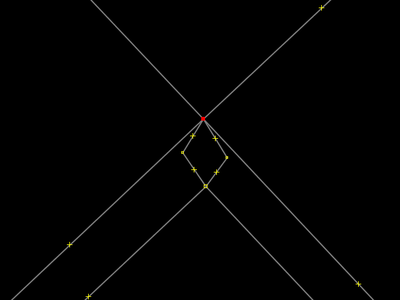
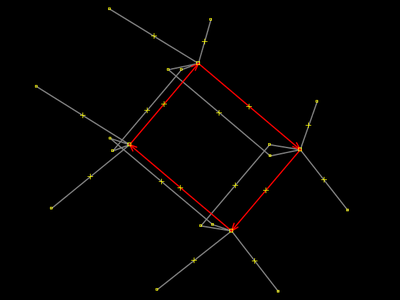
O ponto que está selecionado é uma de duas interseções entre duas ruas que não são mais retas (veja 14 e 16), e é canto do retângulo que representa nossa praça, como sabemos. Os três outros cantos do retângulo não aparecem na imagem mas também estão selecionados, porque o operador pressionou a tecla g com aquela área selecionada. g fez a área desgrudar das ruas, e a seleção deixou de ser nela para ser nos pontos. Se você está confuso, reveja os passos 1, 2 e 3 de #Desgrudar, mover e extrudar. É a mesma coisa! Passar adiante e observar a próxima imagem também poderá lhe ajudar. |
|
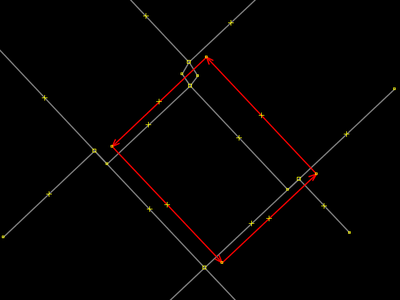
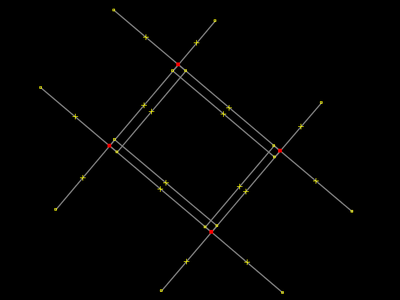
Depois de desgrudada, o operador selecionou a área novamente e a moveu para o lado. |
|
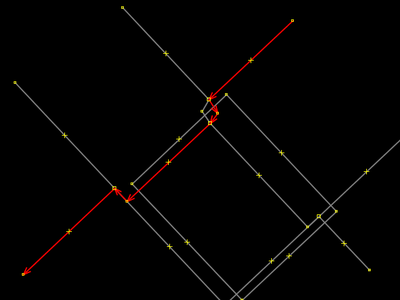
O operador selecionou a rua de cima. |
|
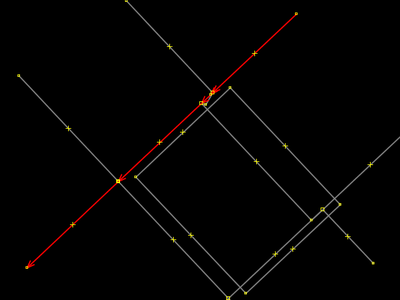
Então o operador teclou L e a rua ficou endireitada. É a mesma coisa de Ferramentas → Alinhar Nós em linha. |
|
Análogo ao passo 14. O operador selecionou a rua lateral. |
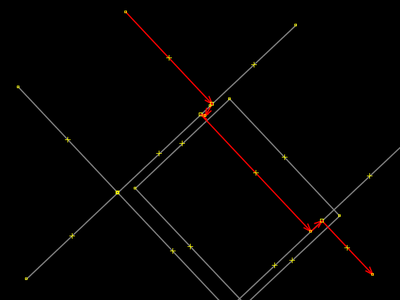
|
Análogo ao passo 15. O operador teclou L e a rua ficou endireitada. Novamente: teclar L é o atalho para Ferramentas → Alinhar Nós em linha. |
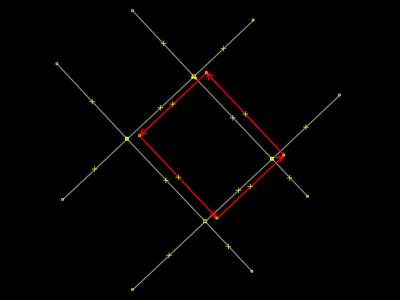
|
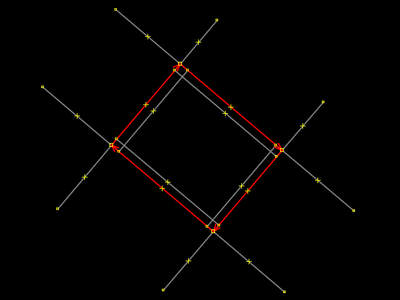
Apague os dois pontos selecionados. Repita tudo para os outros três cantos do retângulo, deixando todas as ruas endireitadas com L. Depois execute o que aprendera nos passos 4 e 5 de #Desgrudar, mover e extrudar: as duas extrusões de redimensionamento do retângulo. Você deverá alcançar um resultado final que "visualmente" pareça-se com esta imagem. Concluindo este passo, podemos considerar que aprendemos nosso primeiro método de extrusão de "praças artísticas", um método básico que leva em consideração uma situação ideal (didática) em que se lida com um "retângulo perfeito", de ângulos retos. |
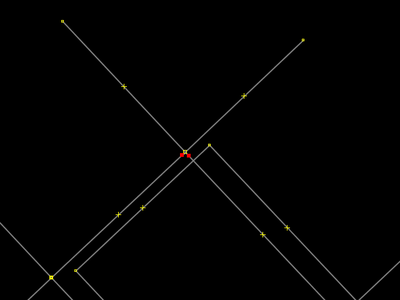
|
O autor original deste tutorial espera que tenha ficado claro que satiricamente denominamos "praça artística" o resultado indesejável de uma prática ruim de mapeamento para o renderizador. As quatro primeiras praças que ele mapeara no projeto OpenStreetMap embutiam esse erro. Ao corrigi-las com muito trabalho e atraso, decidiu escrever este tutorial. A proposta é que aprendamos a corrigir nossos próprios erros, por mais complicado que isso possa parecer.
Detalhando comentários superficiais
Mover a área sem os segundos pontos de interseção de ruas
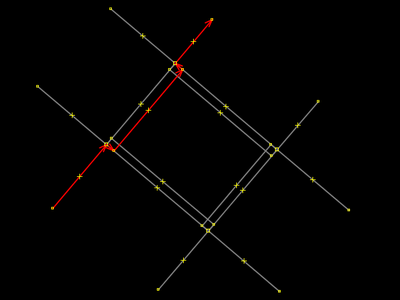
| |
| |
| |
| |
|
Separar em duas áreas com etiquetação confusa
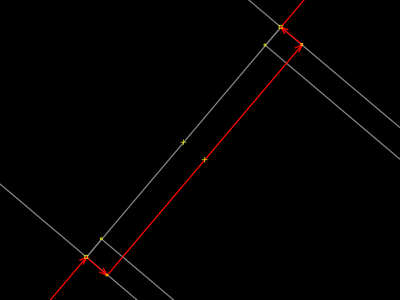
| |
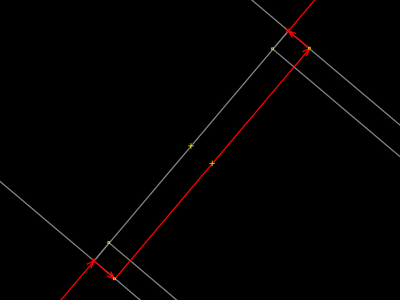
| |
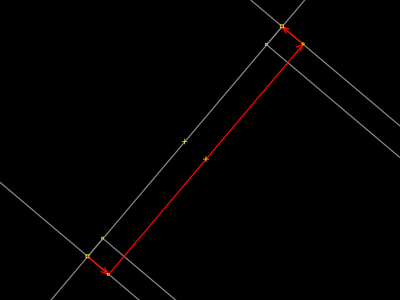
| |
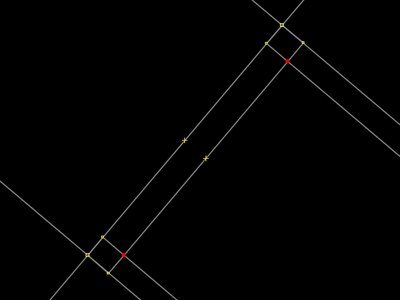
| |
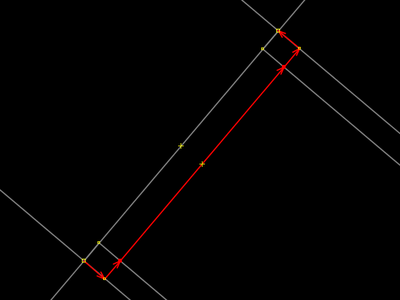
| |
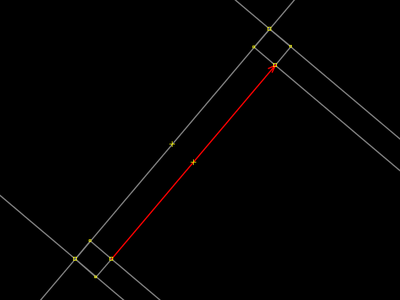
| |
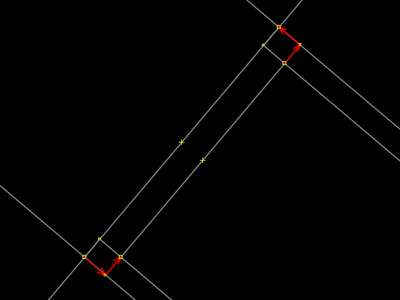
| |
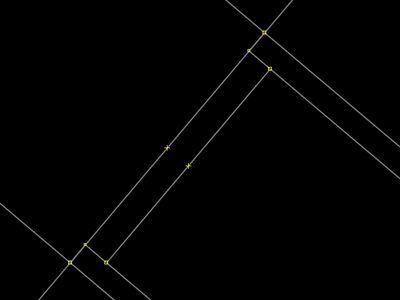
| |
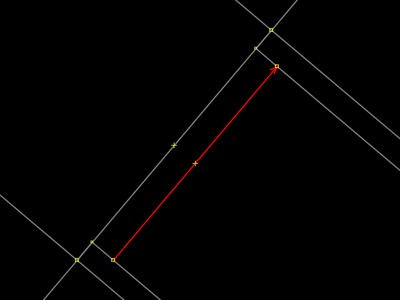
| |
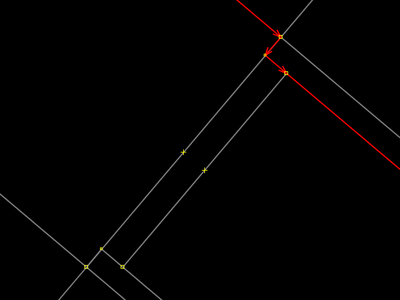
| |
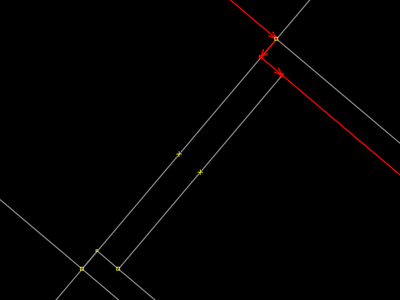
| |
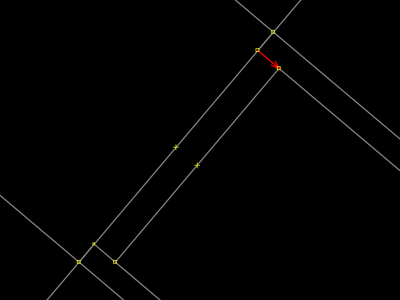
| |
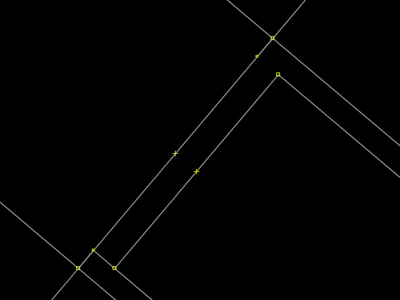
|
Situações reais
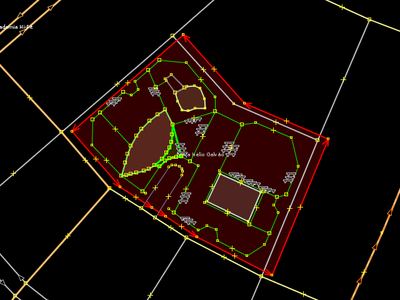
|
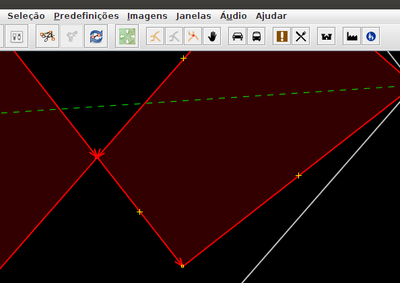
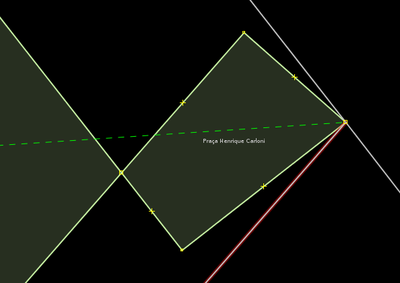
Extrudar e depois eliminar canto
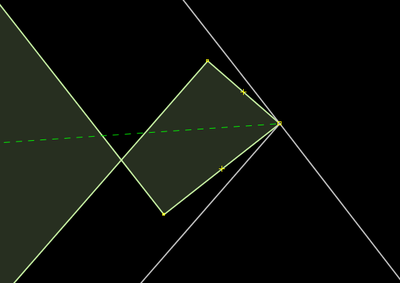
| |
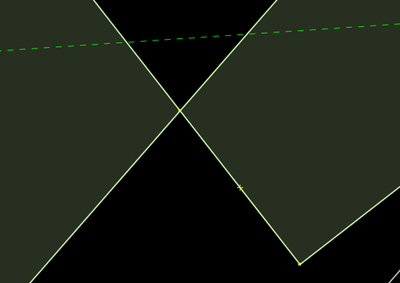
| |
| |
|
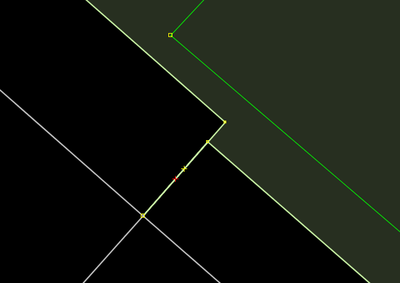
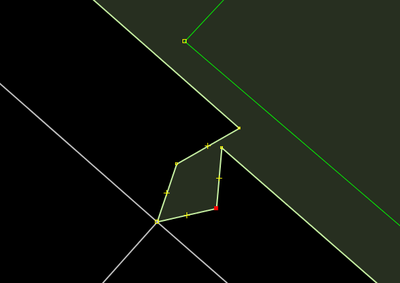
Extrudar e depois eliminar paralelo
| |

| |
| |

| |

| |
| |
|