User:Maxbe/Satteldrehung nach Höhendaten
Worum gehts?
Sättel werden in vielen Karten mit einem Symbol dargestellt, das die Richtung des Sattels angibt. Mit "Richtung" ist hier die gedachte Linie von Tal zu Tal gemeint. Es gibt in OSM auch ein Tag dafür, leider wird direction=* nur selten eingetragen, noch seltener wird es auf unseren Karten dargestellt.
Die beste Lösung wäre natürlich, wir hätten bei jedem natural=saddle auch gleich ein direction-Tag, das dem Renderer die Ausrichtung verrät. Im Januar 2017 haben aber nur 81/26185=0.3% der Sättel, Pässe und Scharten eine eingetragene Richtung. Bis wir das alles gemappt haben, kann der Renderer Sättel nur als ungerichtetes Symbol darstellen oder anderweitig versuchen, die Richtung abzuschätzen:
- Man könnte aus der Richtung der nächstgelegenen Straße die Richtung des Sattels abschätzen. Das funktioniert bestimmt auch bei grossen Pässen wie Brenner- oder Berninapass. Es scheitert aber bei kleinen Sätteln, die bestenfalls von Wanderwegen erschlossen werden. Letztere verbinden oft nicht Tal mit Tal, sondern sind lediglich ein markanter Punkt auf dem Weg den Grat entlang, oder ein Knick, wo der Weg vom Tal auf einen der benachbarten Gipfel schwenkt. Manche Sättel haben überhaupt keinen Weg, sondern sind nur als benamter Orientierungspunkt eingetragen.
- Man könnte die Richtung aus den Höhenlinen abschätzen. Höhenlinien sind bei Renderern häufig anzutreffen, gelegentlich liegen sie sogar in der Datenbank neben den OSM-Objekten. Man sucht sich einfach die nächst niedrigere Höhenlinie und die Verbindungsline von Sattelpunkt zu dieser Linie gibt die Richtung an. Dieses Verfahren gibt es als Versuch, wurde aber nicht weiter verfolgt, weil die vielen geometrischen Abfragen nach Höhenlinien sich als Performancekiller erwiesen haben.
- Man könnte aus den benachbarten Höhenmesspunkten die Richtungen mit Steigung und Gefälle berechnen und daraus die Richtung abschätzen. Dieses Verfahren wird bereits verwendet. Bisher allerdings mit Höhenwerten in einer Datenbank, die kaum jemand vorrätig hat. Deshalb wird hier ein ähnliches Verfahren mit Höhenwerten aus einen GeoTiff vorgestellt.
Verfahren
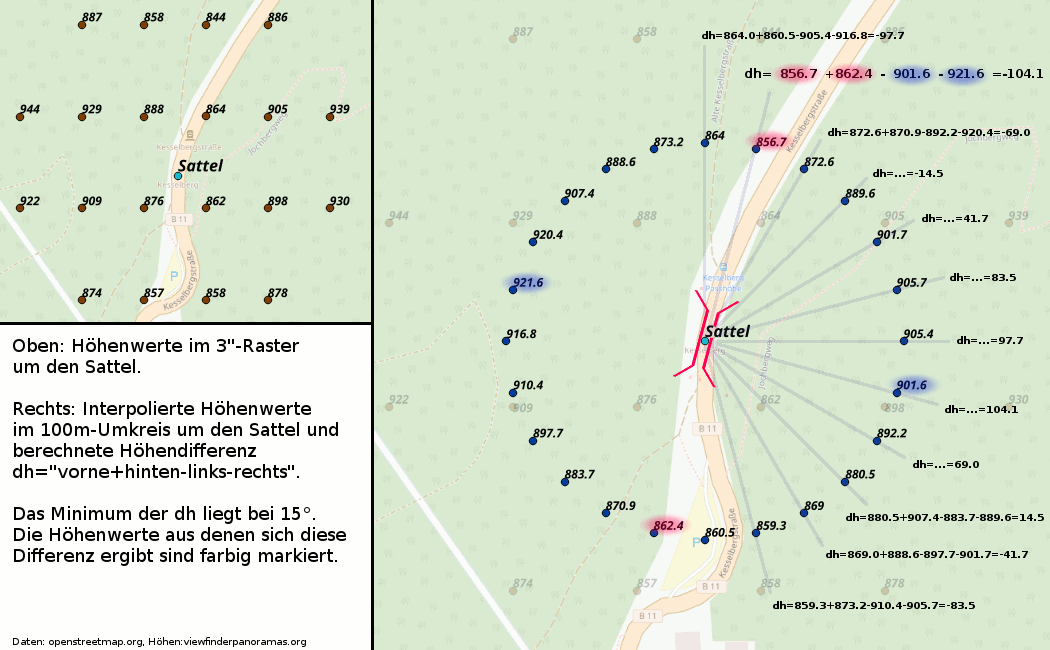
Man berechnet im Umkreis von 100 Metern eine Anzahl von Höhenwerten durch Interpolation aus dem GeoTiff. Dann berechnet man für jede Richtung den Wert "Höhenwert in Blickrichtung + Höhenwert im Rücken - Höhenwert auf der linken Seite - Höhenwert auf der rechten Seite". Der Pass zeigt in die Richtung, in dem dieser Wert minimal ist, denn dort geht es hinten und vorne am weitesten runter und links und rechts am weitesten rauf.
Beispiel
Oben sind rot die Höhenwerte aus den SRTM-Daten abgebildet. Die liegen im 3-Bogensekunden-Raster vor, was in der Gegend um den 48. Breitengrad etwa 90x60 Metern entspricht. Aus diesen Werten werden die Höhen entlang eines Kreises mit 100m Radius um den Sattel berechnet (blaue Punkte im Bild rechts).
Danach wird für den Halbkreis "Nord-Ost-Süd" für jeden dieser Messwerte die Höhendifferenz "vorne + hinten -links -rechts" berechnet (die Zahlen am Ende der Strahlen). Im Beispiel hat der zweite Messwert bei 15° gewonnen. Diese Richtung gibt also die Richtung des Sattels an.
Man muss nur einen halben Kreis berechnen, weil die Symbole für Sättel symmetrisch sind. Falls er Richtung Nordost zeigt, zeigt er auch nach Südwest. Ausserdem muss man nur im ersten Viertelkreis die Höhendifferenzen wirklich ausrechnen, das zweite Viertel hätte die gleichen Werte, nur mit umgekehrten Vorzeichen. Die meiste Rechenzeit wird allerdings für die Interpolation der Höhen verwendet, dort muss man leider den ganzen Kreis durchlaufen, in der echten Welt ist die Landschaft nicht symmetrisch.
Probleme
- Die Höhenwerte müssen zu den Daten der Sättel passen. Das tun sie aber oft nicht. Zum einen, weil frei verfügbare Höhendaten schlicht zu grob sind, um Feinheiten der Landschaft zu erfassen, oder verschoben sind, oder einfach falsch. Zum anderen, weil die Sättel oft nicht am wirklichen Sattelpunkt gemappt wurden. Letzteres könnte ein Versehen des Mappers sein, aber auch Absicht des Strassenbauers. Wege werden oft nicht über die feuchte Wiese am tiefsten Punkt geführt, sondern ein Stück oberhalb. Dort wird dann das Schild aufgestellt und der Kiosk eingerichtet und der Punkt mit dem Schild wird als "Sattelpunkt" angenommen. Der Wiki-Eintrag zu natural=saddle macht den Unterschied deutlich zwischen dem "mountain_pass=yes" auf dem Weg und dem "natural=saddle" auf dem tiefsten Punkt. In der Praxis werden die beiden Punkte aber fast immer zusammengelegt.
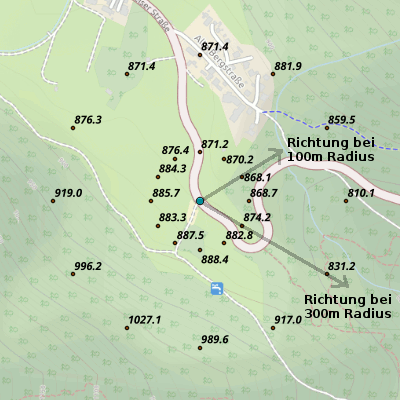
- Der Sattel könnte in einer flachen Gegend liegen, wo der hier verwendete 100m-Radius für die Bestimmung der Ausrichtung nicht passt. Beim Bild rechts führt die Berechnung zu einer um 60° verdrehten Richtung. Würde man einen 300m-Radius nehmen, hätte man ausreichende Höhenunterschiede um die plausibel erscheinende Richtung zu berechnen. Umgekehrt könnte es aber auch sein, dass nach 300m schon der nächste Berg kommt oder sich das Tal krümmt...
- Die Frage nach der Richtung eines Sattels ist auch vom Maßstab abhängig. Bedeutende Gebirgsübergänge würde man bei kleinem Maßstab vielleicht eher generalisiert quer zum Gebirge darstellen, auch wenn in der unmittelbaren Umgebung des Sattels das Tal etwas schräg zur Querungsrichtung liegt.
Lösung aller Probleme
Einfach die direction=* mappen und gut ists... ;)
Programm
Höhendaten
Die Daten stammen aus dem SRTM-Datensatz des USGS (version 2.1)oder den Daten von viewfinderpanoramas.org und wurden entsprechend der Anweisung für die OpenTopoMap runtergeladen und als GeoTiff gespeichert:
gdal_merge.py -n 32767 -co BIGTIFF=YES -co TILED=YES -co COMPRESS=LZW -co PREDICTOR=2 -o ../../DEM.tif *.hgt.tif
wichtig ist hier das "TILED=YES", das später recht performanten Zugriff auf einzelne Höhenwerte ermöglicht.
Quellcode
Findet man im github der OpenTopoMap.
Compilieren
Ausserdem braucht man einen C-Compiler und die GDAL-Bibliothek dafür (bei debian oder ubuntu ist das das Paket "libgdal-dev") zum Übersetzen:
cc -o saddledirection saddledirection.c -lgdal -lm
Testen
Das Programm erwartet eine ;-getrennte Liste aus ID;LON;LAT;direction und gibt eine ebensolche Liste aus. direction kann natürlich auch leer sein und wird vom Programm ausgefüllt. Als Parameter wird mindestens die Angabe der Datei mit den Höhenwerten erwartet.
Richtung des Brennerpasses:
echo "508401093;11.506699;47.007399;" | ./saddledirection -f data/DEM.tiff 508401093;11.5066990;47.0073990;24 echo "508401093;11.506699;47.007399;NNE" | ./saddledirection -f data/DEM.tiff 508401093;11.5066990;47.0073990;22 echo "508401093;11.506699;47.007399;23" | ./saddledirection -f data/DEM.tiff 508401093;11.5066990;47.0073990;23 echo "508401093;11.506699;47.007399" | ./saddledirection -f data/DEM.tiff -o sql update planet_osm_point set direction='24' where osm_id=508401093;
Für Besitzer einer Datenbank
psql -A -t -F ";" osm -c "select osm_id,st_x(st_astext(st_transform(way,4326))),\ st_y(st_astext(st_transform(way,4326))),direction from planet_osm_point where osm_id=508401093;"\ | ./saddledirection -f ../DEM.tiff -o sql update planet_osm_point set direction='24' where osm_id=508401093;
Ein Pass in der Nähe des Nordpols
echo "123;0;89;" | ./saddledirection -f data/DEM.tiff 123;0.0000000;89.0000000;-135
Der Nordpol liegt ausserhalb des Bereiches, der von den Höhendaten abgedeckt wird. Als Ergebnis wird -135 zurückgegeben. Daran kann man erkennen, dass ein Fehler vorlag (weil negativ, berechnete Ergebnisse sind 0..179). Allerdings kann man das trotzdem z.B. einem Renderer vorlegen, der würde dann das Symbol von links unten nach rechts oben zeichnen. Die gleiche Ausgabe -135 bekäme man, wenn man Stellen in der Geotiff-Datei hat, die unter -32000 liegen. Üblicherweise werden Stellen ohne Daten mit dem Wert -32768 markiert.
Kommandozeilenparameter
- -f datei geotiff-Datei mit den Höhenwerten. Sie muss genau ein Band mit "Type=Int16" haben. Falls man hgt-Dateien umwandelt, bekommt man eigentlich immer dieses Format. Ausserdem muss sie in EPSG 4326 vorliegen. Sie muss nicht die ganze Erde abdecken.
- -n schritte Gibt die Anzahl der Höhenpunkte für den Kreis an. Bei 12 Punkten bekäme man die Richtung in 30°-Schritten, bei 360 auf ein Grad genau. Defaultwert ist 60.
- -r radius Gibt den Radius für den Kreis an. Default ist 100.
- -o format Gibt das Ausgabeformat ("csv" oder "sql"). Default ist "csv". "Bei "sql" wird ein SQL-Befehl für jeden Sattel ausgegeben ("update planet_osm_point set direction='23' where osm_id=508401093;"), mit der man seine Datenbank aktualisieren könnte.
- -d level Gibt den Debuglevel an, (0-4), default ist 0. Ist vielleicht nützlich, wenn man wissen will, wie ein Ergebnis zustande kommt.
Laufzeit
Etwas betagtere Rechner sollten auf ein paar hundert Berechnungen pro Sekunde kommen, neuere Rechner auf 1000-3000. Momentan (Jan 2017) gibt es etwa 27000 Pässe, Sättel und Scharten. Die sollten nach einigen Sekunden berechnet sein.
Richtungen zum Runterladen
Wer das Programm und die Höhendaten nicht selbst installieren mag, kann sich die Höhendaten auch runterladen. Drei Dateien mit 50 Meter, 100 Meter und 200 Meter Radius und jeweils 60 Schritten auf Basis der 3"-SRTM-Daten werden alle paar Tage neu berechnet und enthalten sämtliche OSM-Pässe, Sättel und Scharten.
Diese SRTM-Daten enthalten leider ein paar Stellen ohne Daten, dummerweise oft im steilen Gelände. Vielleicht findet man auch bessere Höhendaten, die man für diese Zwecke verwenden und zusammen mit Openstreetmap-Daten zur Verfügung stellen kann.
Wegen der Lücken und aus oben genannten Gründen sind diese Daten nicht dazu geeignet in OSM übernommen zu werden, Sättel sollten also weiterhin mit Ortskenntnis oder sogar im Rahmen eines Besuchs vor Ort gemappt werden. zur Erzeugung hübscher Karten sind sie aber vielleicht gut genug...
Für die OpenTopoMap werden die Höhendaten von Viewfinder Panoramas verwendet. Mit freundlicher Genehmigung von Jonathan de Ferranti können wir auch die daraus erzeugten Sattelrichtungen veröffentlichen (50, 100 und 200 Meter)